A Lightning-Fast INDEX Drives Massive DATA Analysis

September 11, 2009

FastBit is an extremely efficient indexing technology for accelerating database queries on massive datasets. FastBit enhances conventional bitmap indexing technology by employing advanced compression, encoding, and binning methods. Previously, bitmap indexes were only considered useful for categorical data with a small number of possible values. Now, many applications (especially scientific applications) require indexing over data with a very large number of possible values. Because of specialized enhancements, FastBit is fast enough to support real-time queries for scientific data exploration applications, such as visual analytics. In many applications, FastBit can search data 10–100 times faster than other products.

As computers become ever more powerful, they collect and produce more bytes of data. Making sense of all the bytes is becoming a central challenge of many scientific endeavors. Often, a small fraction of the data records holds the key to insight; therefore, an efficient tool to locate and retrieve key data records is essential. In the past 30 years, database management systems have emerged in industry as the most prevalent tools for such tasks.

A database management system imposes certain structures on the data records, typically as tables with rows and columns, and requires all questions (queries) to be in a machine processable language, such as the Structured Query Language (SQL). The system optimizes the query-answering process by implementing auxiliary data structures to accelerate common types of questions. These acceleration techniques are known as database indexes. FastBit is one such database indexing system, designed primarily for answering queries efficiently.

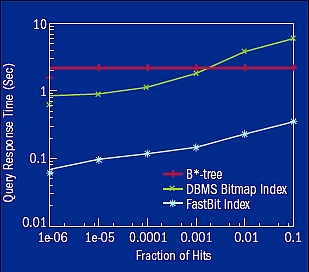
Figure 1. The average query response time measured on the client to answer the same set of queries on a set of high-energy physics data. Both B*-tree and the database management system bitmap index are from well-regarded commercial database management systems. Bitmap indexes from both the database management system and FastBit are compressed basic bitmap indexes; the only difference is the compression method used. Across the whole range of queries, FastBit is on average 14 times faster than the commercial bitmap index. The FastBit index is 4–30 times faster than the B*-tree.

FastBit can search huge databases much more quickly than the fastest commercially available database management system (figure 1). For example, researchers from the University of Hamburg, Germany used FastBit to accelerate their drug discovery software by 140–250 times. Engineers at a major Internet company found that FastBit can match Web pages with advertisements at least 10 times, and in many cases 100 times, faster than commercial database technologies. And visualization experts at Lawrence Berkeley National Laboratory (LBNL) showed that FastBit can identify and track particles in a laser wakefield particle accelerator simulation 1,000 times faster than previous tools. In addition, academic groups and commercial companies use FastBit for activities such as image analysis, computer network security, national security, and routing of Voice over Internet Protocol (VOIP). FastBit’s efficient search capability is critical to these applications.

FastBit was originally designed to help particle physicists sort through billions of data records to find a few key pieces of information. For example, in a high-energy physics experiment called STAR, colliding particles generate billions of collision events, but only a few hundred of these might have the most distinctive signatures of a new state of matter—called quark–gluon plasma—and finding evidence of this plasma is a major objective of the STAR experiment.

In such an application, the dataset includes hundreds of searchable attributes, and the base data records are not updated once they are generated. In contrast, the common transactional applications for which the database systems were designed typically contain only a small number of searchable attributes. For example, a banking application might only be able to search for accounts based on account number and customer name. In addition, a database management system is designed to locate an individual record (or a very small number of records) efficiently, while most scientific data analysis tasks require a much larger number of records. Furthermore, scientific data analyses are much more ad hoc, where users usually examine many combinations of conditions on different attributes. All of these present tremendous challenges for existing indexing methods.

Of the many indexing methods intended to accelerate search operations, the most popular is the B-tree index. However, B-tree indexing methods fail to meet the stringent demands of modern data analysis, such as interactive visual analysis over terabytes of data, or locating the mastermind behind distributed denial-of-service attacks while the attacks are in progress. These queries return thousands of records that require a large number of tree-branching operations that translate into slow pointer chases in memory and random accesses on disk, thus taking a long time.

One reason for this behavior is that these tree-based indexing structures are designed for data that change frequently over time. They are optimized for finding a very small number of records, such as finding a bank account and updating the balance. They are not well-suited for locating thousands of records, as is necessary in a typical analysis of large datasets. Many popular indexing techniques, such as hash indexes, have similar shortcomings. Furthermore, B-tree indexes inflate the volume of the data stored by a factor of three to four, which is not generally acceptable when dealing with terabyte-sized datasets.

B-tree and variants are primarily designed for searching one variable at a time. For searching multiple variables simultaneously, other tree-based indexing techniques, such as Oct-tree and KD-tree indexes, are more appropriate. Such indexes are designed for queries that involve all variables indexed. In many applications, the user only searches on a handful of variables out of hundreds. In these cases, these tree-based indexes are very ineffective. In scientific applications where users often query on an arbitrary combination of variables, limiting searches to any subset of combinations may limit the possibility of discovery. To meet all these demands, another type of index must be used.

For tasks that demand the fastest possible query processing speed, bitmap indexes have shown promise after a number of years of active use in some commercial database management systems (sidebar “Bitmap Index: An Example” p33). However, the effectiveness of these bitmap indexes is limited to certain types of data, primarily those variables with a relatively small range of possible values, such as the gender of a customer or the state in which the customer lives. These variables with a relatively small number of possible values are known as categorical values, or low-cardinality variables. However, most scientific data contain variables—such as velocity, temperature, and pressure—that have a very large number of possible values. FastBit significantly improves the speed of a searching operation on both high- and low-cardinality values with a number of techniques, including a vertical data organization, an innovative bitmap compression technique, and several new bitmap encoding methods.

Vertical Data Organization

The first technique used in FastBit is vertical data organization. The use of this technique grew out of the need to search on a relatively small number of variables from a massive dataset with a large number of searchable attributes.

For example, the first application we tackled was a high-energy experiment that produced billions of data records, or “events,” each associated with hundreds of searchable variables. However, a typical search only involves a handful of variables, making it highly desirable to partition the data by variable and to store their values in separate files to avoid reading unnecessary data from disk. This way of organizing data, known in the database community as “vertical partitioning,” is well-suited for scientific applications and data warehousing applications where existing records are not modified.

In contrast, the traditional horizontal data organization makes it necessary to retrieve all variable values of a record if any values are needed. The horizontal data organization is well-suited for transactions, such as recording changes in a department store’s inventory. However, a scientific data analysis is very rarely such a transaction. In most cases, a scientific dataset like a commercial data warehouse is modified through append operations only, and the majority of queries only touch a subset of the variables. The vertical data organization is well-suited for such data access patterns.

Word-Aligned Hybrid Compression

The second key technology in FastBit is an innovative compression method called Word-Aligned Hybrid (WAH) compression. It reduces index sizes by compressing each individual bitmap separately, while at the same time allowing operations on the compressed bitmaps to proceed efficiently.

Typically, a bitmap index resides on a disk file system or another secondary storage system. To answer a query, the relevant part of the index is read into the computer’s memory before computation. The conventional wisdom is that the time needed to read parts of the index into memory is much greater than the time needed to perform the computation after the data are in memory.

However, with existing compression techniques, answering a query using compressed bitmap indexes in fact requires more time to perform computations on the bitmaps than the time to read these bitmaps into memory. Therefore, the most direct way to improve the efficiency of compressed bitmap indexes is to make the computations on the compressed bitmaps faster. WAH was invented and patented in 2004 specifically for this purpose. See the sidebar “FastBit Compression” for more information about this specialized compute-efficient compression method.

In many tests, WAH-compressed indexes have been shown to be 10 times faster than the best-known bitmap indexes. In addition to being compute-efficient, WAH is also effective in reducing index size. The size of a FastBit index is on average one-third the size of the original data, which is about one-tenth the size of the widely used B-tree index.

Encoding Methods for Bitmap Indexes

The third key technology in FastBit is a new group of bitmap encoding methods called multi-level encodings. A multi-level encoding method employs a nested set of bins to reduce the amount of work required for answering a query. In this case, higher levels of a multi-level index can give an approximate solution and lower-level indexes are accessed as needed to refine the solution.

For a number of years, various attempts have been made to construct multi-level encodings; however, none of them has been shown to be definitively more efficient than simpler encoding methods. Recently, through extensive analyses, FastBit developers found that optimal performance can be achieved with only two levels, and the best of the two-level encodings can perform, on average, three to five times faster than the best one-level indexes with WAH compression.

Basic Encoding Methods: Equality, Range, and Interval Encoding

In general, a bitmap index can be constructed in three steps: binning, encoding, and compression. In the binning step, each variable of the base data is scanned and grouped into bins. For example, for a string-valued variable, strings starting with the same character may be grouped into a single bin; for a floating-point valued variable, such as pressure, all the values with the same exponent may be grouped into a single bin. The encoding step takes the bin identifiers and translates them into bitmaps. For example, the integer variable X shown in figure 2 (p33) may be viewed as bin numbers. The encoding method used by the basic bitmap index is known as the equality encoding because each bitmap represents exactly one bin. If a value for a particular row falls in a bin, a 1 is placed in the corresponding position of the bitmap.

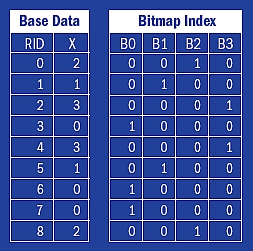
Figure 2. A logical view of the basic bitmap index for a variable named X. Columns B0–B3 are bitmaps.

When each bin contains exactly one value, the equality encoding can be thought of as storing pre-computed answers to equality queries of the form X = a, where a is one of the values that appeared in the dataset for variable X. For a query of the form a≤X≤b, many equality encoded bitmaps are needed. In general, the wider a query range [a, b] is, the more bitmaps are needed.

Another popular encoding method is range encoding, which can be viewed as storing pre-computed answers to range queries of the form X ≤ a. Its first bitmap is the same as the first bitmap under the equality encoding; its second bitmap is the bitwise OR of the first two bitmaps under the equality encoding; and its third bitmap is the bitwise OR of the first three bitmaps under the equality encoding. In general, the kth bitmap under the range encoding is the bitwise OR of the first k bitmaps under the equality encoding.

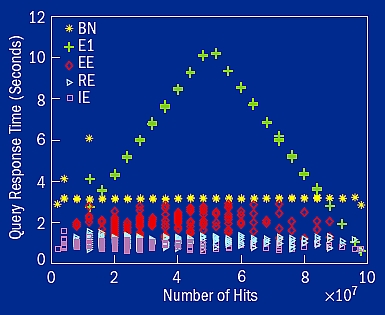
Figure 7. Query response time of the five best bitmap encoding methods available from FastBit: binary encoding (BN), one-component equality encoding (E1), equality-equality encoding (EE), range-equality encoding (RE), and interval-equality encoding (IE). Time is measured on a set of 100 million rows of uniform random data. We observe that the two-level encoding methods (EE, RE, and IE) never took more time to answer the same query than the binary encoding and the one-level equality encoding. On average, the intervalequality (IE) encoding is 4.3 times faster than the binary (BN) encoding.

A third well-known encoding method is interval encoding, which can be thought of as pre-computing a subset of queries of the form a ≤X ≤ b. Under interval encoding, each bitmap is the bitwise OR of about half of the bitmaps under the equality encoding. Given 100 bins, the equality encoding produces 100 bitmaps, but the interval encoding produces 51 bitmaps. The first bitmap under the interval encoding is the bitwise OR of the first 50 bitmaps under the equality encoding. The second bitmap is the bitwise OR of 50 bitmaps under the equality encoding, starting with the second bitmap. In general, the kth bitmap under the interval encoding is the bitwise OR of half of the bitmaps under the equality encoding starting with the kth bitmap.

One advantage of interval encoding is that the number of bitmaps is about half that of the equality and the range encoding. Due to its unique construction, it is possible to answer any query of the form a ≤ X ≤ b with two bitmaps. It is possible to answer the same query with two bitmaps under the range encoding as well. However, because the interval encoding produces less bitmaps, we would prefer the interval encoding in general.

In practice, interval encoding is not widely used. Ten years after it was proposed in the research literature, no commercial database system has implemented it because the interval-encoded bitmaps do not compress well. Even with the best possible compression method, the size of an interval-encoded index could be much larger than the base data.

Multi-Component Encoding

A strategy to curb the index size is to split a bin number into multiple components. For example, with 1,000 bins numbered from 0 to 999, one may split the three-digit number into three components where each decimal digit is considered a single component and encode each of the three components separately. Under the equality encoding, one needs 10 bitmaps for the first (most-significant) digit, 10 bitmaps for the second digit, and 10 for the third (least-significant) digit. Altogether, it uses a total of 30 bitmaps under the three-component equality encoding instead of 1,000 under the simple equality encoding. The number of bitmaps needed for three-component range encoding and interval encoding can be reduced similarly.

The number of bitmaps generated by multi-component encoding decreases monotonically as the number of components increases. With range encoding and the interval encoding, index size decreases proportionally as well. In the extreme case, where the maximum number of components is used, each component includes two possible values, which is equivalent to breaking the bin numbers into individual binary digits. In this case, because the two bitmaps representing a binary digit are complements of each other, it is possible to retain only one of the two bitmaps for each component. Retaining the bitmap corresponding to the binary digit being 1 is equivalent to a popular encoding method called binary encoding; the corresponding index is known as the bit-sliced index. It turns out that binary encoding is better than the multi-component versions of all three basic encoding methods—equality, range, and interval encodings—with the exception of the one-component equality encoding. We have proven these results theoretically and observed them in practice.

In short, among all multi-component encoding methods, there are two that perform better than others: one-component equality encoding and binary encoding. This distinction is also reflected in the fact that these are the only encoding methods used in commercial database management systems. FastBit uses these multi-component encodings.

Multi-Level Encoding

In addition to the encoding methods described so far, FastBit also includes a number of multi-level encodings that outperform the best of these multi-component encoding methods. These multi-level encodings are constructed on a hierarchy of bins with coarser bins on top and finer bins at the bottom. Each level of a multi-level index can be encoded independently. When answering a query, we generally use the coarser level indexes first to get an approximate answer and use finer levels to identify the records that cannot be resolved with the coarse levels. In this process, a fine-level index is used to resolve a range condition with a narrower range and involving a smaller number of records. Because only equality encoding can use fewer bitmaps to resolve a narrower range condition, a multi-level index can only use the equality encoding at the fine levels.

An example of multi-level encoding is the interval-equality encoding that uses a set of very coarse bins with the interval encoding and a set of fine bins with the equality encoding. Because the interval encoding only has a very small number of bins at the coarse level, the total size of the bitmaps is modest. At the same time, interval encoding can answer queries quickly, and we only need to examine a small number of fine-level equality encoded bitmaps to get the final answer. Therefore, the interval-equality encoding combines the best characteristics of both the interval and equality encoding.

Similar multi-level encodings can be composed for other combinations. In figure 7, the timing of three such two-level encodings is shown against two of the best multi-component encodings. When a query selects a relatively small number of records, say less than 10% of all records, which is 10 million of the 100 million records in the test presented in figure 7, the binary encoding is slower than four other methods because it requires all the bitmaps to answer a query. In figure 7 the number of records selected by a query is referred to as hits for the query. The number of hits increases, the basic equality encoded index needs to work with more and more bitmaps in order to produce the answers, and it takes more time than the others. In all cases, we see that the three two-level indexes take less time than the bit-sliced index and the basic bitmap index, the two best multi-component encodings.

The interval-equality encoding (IE in figure 7) is on average four times faster than the binary encoding (BN) and seven times faster than the one-component equality encoding (E1). The performance advantages of these two-level encodings are not only observed in timing measurements, but are also verified with extensive theoretical analyses.

In summary, the combined use of multi-component interval-equality encoding with the WAH compression yields 50-fold speedup as compared to the best known bitmap indexes. The WAH compression provides a 10-fold performance gain, and the multi-component encoding provides an additional five-fold improvement. Given that bitmap indexes perform well for data that do not change over time (append-only data) they are generally faster than any other known indexing methods, such as tree-based indexes. Consequently, FastBit is sufficiently fast for real-time search applications over large datasets. Thus, it is particularly useful for dynamic real-time data exploration and visualization applications.

Unique Design, Impressive Performance

Combining WAH compression and two-level encoding yields an outstanding speedup of 30–50 times faster relative to the widely-used bitmap indexing methods, including those from the most popular commercial database management system products.

Another unique feature of WAH-compressed indexes is that they are amenable to theoretical analysis. Through analyses, WAH-compressed indexes, including the WAH-compressed basic bitmap index and some of the new multi-level bitmap indexes, have the same theoretical optimality as the best of the B-tree variants. That is, the search time is bounded by a linear function of the number of records that satisfy the search criteria, called hits. In theory, the time required by the best of the B-tree indexes is also bounded by a linear function of the number of hits, but FastBit is 20–100 times faster than B-trees from commercial database management system products. This difference is because the size of the FastBit index is much smaller and the logical operations are very fast on modern computers (compared with tree-branching operations). Furthermore, FastBit performs extremely well on multi-variable queries because the intersection between the search results on each variable is a simple AND operation over the resulting bitmaps.

The combination of compression and binning works especially well for scientific data, where the majority of the variables have high cardinalities. This design also works well for those data with lower cardinalities, such as those from commercial data warehouses, medical applications, and network traffic logs. FastBit search time was proven with both theoretical analyses and timing measurements to be proportional to the compressed sizes (bytes) of bitmaps involved in a search. Because the total size of compressed bitmaps is modest for high-cardinality values, the total search time is also modest. The binning strategy is useful for high-cardinality data as well as multi-level encoding. FastBit implements a variety of binning options for extremely high-cardinality values. This ability to index high-cardinality data is unique to FastBit and is not supported by other bitmap indexing methods.

FastBit has been applied to a variety of applications, including simulation and experimental data from climate modeling, high-energy physics, astrophysics, biological sequences, satellite imaging, and fusion. Recently FastBit was also demonstrated to be helpful in real-time visual exploration, referred to as visual analytics. Using FastBit indexes significantly reduces the time needed for exploring a large dataset. After a user modifies the search parameters, the new results can be displayed in real-time, making the exploration process truly interactive. For example, a scientist looking for the features of flame fronts in a combustion simulation can interactively vary the search parameters on temperature and various chemical species to understand how flame fronts behave and progress over time. An example of visual analytics on laser wakefield particle accelerator simulation data is given in the sidebar “FastBit in Visual Analytics” (p36).

To summarize, FastBit has been proven to be theoretically optimal, and it performs 10–100 times faster than any known indexing methods. The key technologies that enable such impressive performance include the use of a patented compression method, advanced bitmap encoding methods, binning, and vertical data organization. These unique characteristics have made it extremely useful in a variety of applications.

Figure 8. Three developers of FastBit at the R&D 100 award ceremony. Left to right, Kesheng Wu, Arie Shoshani, and Ekow Otoo, all from LBNL.

FastBit software was packaged in 2007 and released under an open-source software license. Since its release, it has attracted interest in many new application areas, including computer network security from International Computer Science Institute, drug discovery from University of Hamburg, Germany, Web content delivery, VOIP traffic routing, and web traffic analyses. In 2008, it received a R&D 100 award, which recognizes the 100 most innovative products for that year by R&D Magazine (sidebar “FastBit Wins R&D 100 Award”).

Contributors

Kesheng Wu, Arie Shoshani, and Ekow Otoo, all at LBNL