Applied mathematics involves using mathematical approaches and techniques to solve real-world problems in specialized fields such as physics, biology, computer science, and engineering. Researchers apply mathematical methods to model and simulate physical phenomena—such as fluid flows, electromagnetic devices, materials, future energy, and quantum materials—analyze experimental data and develop innovative machine-learning techniques.

At Berkeley Lab, our mathematics work is highly collaborative. Our applied mathematicians and computer scientists partner with scientists nationwide to design and develop mathematical models and algorithms that address scientific and engineering challenges of interest to the Department of Energy, particularly in the areas of energy and the environment.

We create novel numerical methods to solve mathematical problems more quickly, accurately, and efficiently. Our team develops widely used open-source software for efficient simulations, machine learning strategies, and mathematical approaches for experimental investigations, advancing scientific discovery through collaboration.

Our experts excel in analyzing and solving nonlinear partial differential equations, ordinary differential equations, and stochastic processes. Additionally, our numerical linear algebra specialists develop efficient linear and eigensolver algorithms, along with scalable library implementations. Most of our algorithms are optimized for current and next-generation massively parallel computing architectures.

Our Research Pillars:

  • Discretizations & Methods
  • Interface Dynamics
  • Numerical Linear Algebra
  • Math for Data
  • Mathematical Software
  • Optimization
  • Partial Differential Equations
  • Uncertainty Quantification
 The image displays three colorful, three-dimensional graphs with peaks and valleys, each representing different data sets or functions. The graphs are rendered in vibrant shades of blue, green, and purple, and are positioned against a dark background with faint mathematical equations or diagrams. The visual suggests a focus on data analysis or mathematical modeling.

SuperLU is an open-source library for the direct solution of large, sparse linear systems, providing robust and scalable algorithms essential for high-performance scientific computing and simulation at extreme scales.

 Visualization of the ITER tokamak, the largest fusion device of its kind when built. The image highlights the use of SuperLU and STRUMPACK solvers in simulation codes for projects like ITER, showcasing advanced computational methodologies.

STRUMPACK (STRUctured Matrices PACKage) delivers advanced algorithms for solving large sparse and dense linear systems, leveraging hierarchical matrix compression for exceptional speed and memory efficiency on modern supercomputers.

 The image illustrates a simulation of fluid flow or heat transfer through a porous medium or a channel with obstacles. It features streamlines and color-coded variations representing temperature or pressure changes. The simulation is typical of Computational Fluid Dynamics (CFD) software, used to analyze and visualize complex fluid dynamics scenarios.

PETSc (the Portable, Extensible Toolkit for Scientific Computation) is a suite of data structures and routines for scalable parallel solution of scientific applications modeled by partial differential equations and related problems.

 3D visualization of fluid turbulence simulation inside a transparent, funnel-shaped vessel, showing green and yellow turbulent flow structures.

AMReX is a modern, open-source framework for block-structured adaptive mesh refinement (AMR), designed for exascale computing and next-generation architectures. It enables high-performance, massively parallel simulations of multiscale and multiphysics phenomena in cutting-edge scientific applications.

 A colorful 3D visualization of complex geological formations, featuring vibrant shades of green, blue, orange, and red. The image includes intricate textures and patterns, with black arrows indicating flow directions or data points. This visualization highlights advanced computational techniques used to analyze and interpret geological structures.

Chombo is a robust and flexible AMR framework supporting complex geometries and embedded boundaries, widely used for developing parallel simulation codes in fluid dynamics, plasma physics, and geosciences. It is valued for its extensibility and its support of legacy and industrial applications.

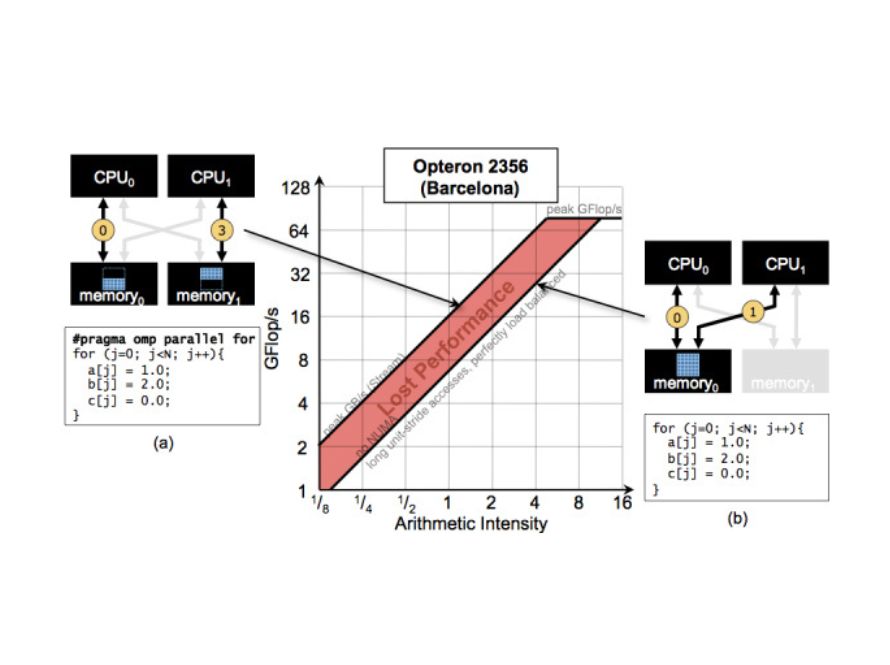
 A performance graph for the Opteron 2356 (Barcelona) processor shows attainable GFLOP/s versus arithmetic intensity, with a red band labeled "Lost Performance" indicating efficiency limits; diagrams and code snippets on either side illustrate different CPU and memory configurations and parallel programming approaches.

The Roofline Model offers an intuitive visual and mathematical framework for analyzing and optimizing code performance on multicore and accelerator-based supercomputers, helping researchers identify and overcome computational bottlenecks.

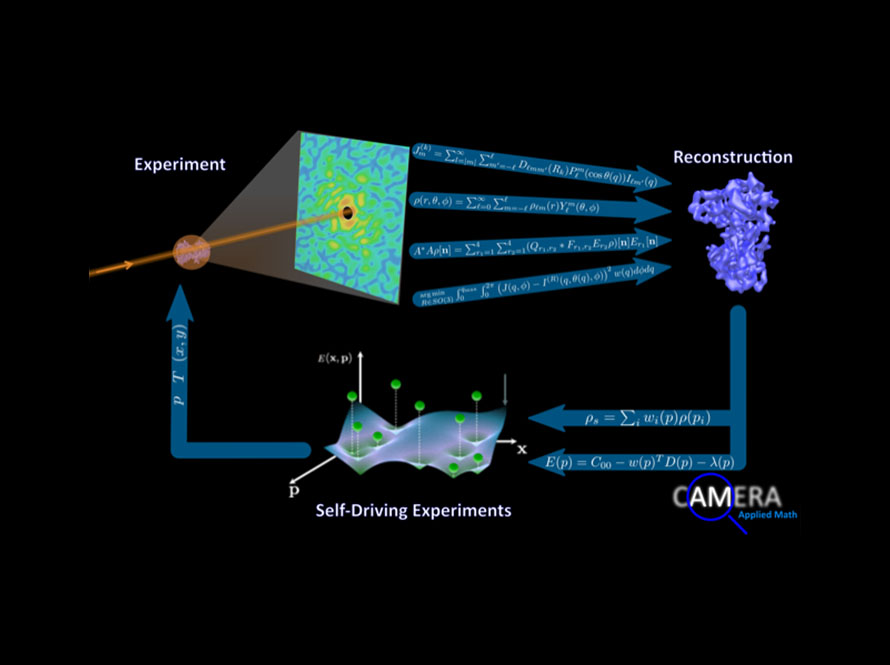
 Diagram illustrating a feedback loop between experiments, mathematical reconstruction, and self-driving experiments. On the left, an experiment produces a complex data pattern, which flows through mathematical equations and leads to a 3D molecular reconstruction on the right. Below, a surface plot represents the optimization process of self-driving experiments, completing the cycle. The CAMERA Applied Math logo is in the lower right corner.

CAMERA invents, develops, and delivers new mathematics for experimental data analysis, imaging, and autonomous experiments, accelerating discovery at national user facilities through advanced algorithms and cross-disciplinary collaboration.

 An artistic illustration of a mixture of Gaussian processes and a light or particle beam passing through. The image represents the inner workings of the algorithm inside gpCAM, a software tool developed by researchers at Berkeley Lab's CAMERA facility to facilitate autonomous scientific discovery. The illustration features a glowing white beam intersecting a surface with multiple peaks and valleys, symbolizing the complex mathematical computations involved.

gpCAM brings advanced mathematics to autonomous experimentation, using Bayesian optimization and machine learning to guide scientific instruments in real time. By mathematically modeling uncertainty and efficiently exploring complex possibilities, gpCAM enables “self-driving” labs that accelerate discovery and make experiments smarter and more efficient.

 Visualization of a complex computational model featuring a lattice structure with hexagonal cells, containing red and blue clusters representing data points or molecular interactions. This image is associated with a paper by Mauro Del Ben and Charlene Yang, recognized as a finalist for the ACM Gordon Bell Prize for achievements in high performance computing.

BerkeleyGW applies cutting-edge mathematical methods to solve quantum mechanical equations, allowing scientists to accurately predict the electronic and optical properties of new materials. This mathematical rigor accelerates innovation in energy, nanotechnology, and computing.

 False-color GIWAXS (Grazing Incidence Wide Angle X-ray Scattering) image showing a curved detector pattern with a distinct missing vertical wedge in the center, representing the region of reciprocal space that is inaccessible due to the projection of the Ewald sphere; bright rings and arcs indicate scattering from the sample, with intensity shown in blue, green, and yellow.

HipGISAXS uses powerful mathematical algorithms and high-performance computing to analyze X-ray scattering data, revealing the nanoscale structure of advanced materials. Its mathematical foundations help researchers unlock new insights for batteries, catalysts, and medical technologies.

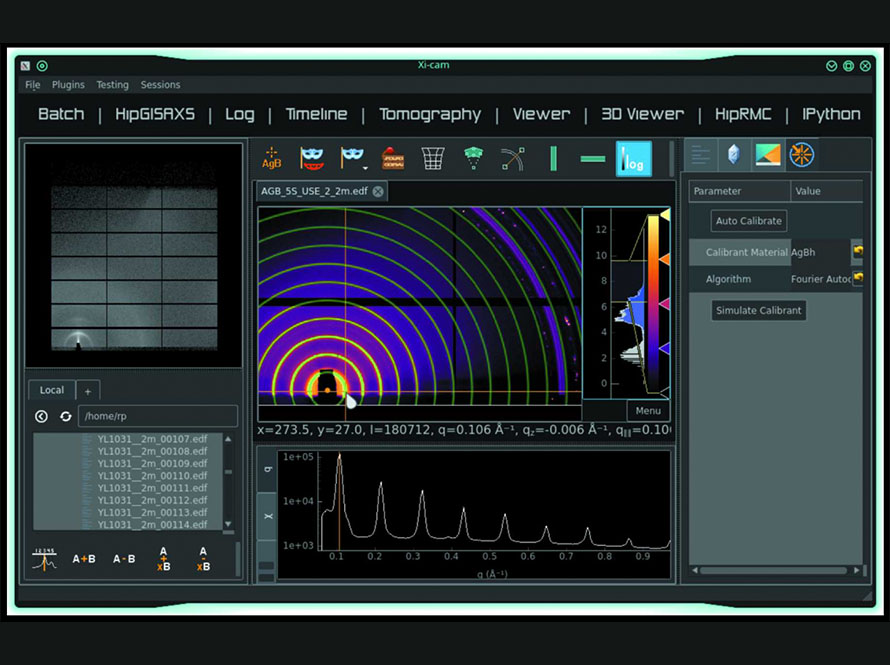
 Screenshot of a scientific software interface showing automated calibration of silver behenate data. The center panel displays overlapping yellow and green rings, indicating alignment, and a graph at the bottom shows the resulting one-dimensional spectrum.

Xi-cam integrates advanced mathematical techniques into user-friendly software that visualizes and interprets complex experimental data from leading research facilities. This mathematical sophistication enables scientists to draw meaningful conclusions from massive, high-throughput datasets.

 A digital background featuring circular, futuristic blue interface elements and geometric patterns along the left and right edges, with a large solid blue rectangle in the center.

ENDURABLE brings mathematical precision to organizing and sharing scientific data for AI and machine learning, developing robust standards and tools that ensure data quality and reproducibility. Its approach empowers researchers to build trustworthy, data-driven scientific discoveries.

 Digitally-generated cross-section of mathematically-simulated water waves. Side-by-side images showing 3D reconstructions of a virus particle. The left image is a smooth, gray, 3D model of the outer shell of the virus, resembling a rounded polyhedral shape. The right image shows a cross-sectional heatmap of the virus interior, with colors ranging from blue/green to yellow/red, indicating variations in density or material, and revealing asymmetries in the internal genetic material. These reconstructions were created using the M-TIP framework based on experimental correlation data.
Last edited: December 22, 2025