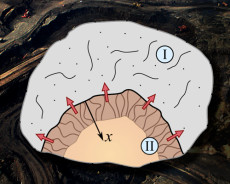
The model developed by Monteiro, Rycroft, and Barenblatt posits a porous, fissurized matrix (I) with enough permeability to be treated by standard fluid mechanics, as well as a kerogen inclusion (II) with very low permeability. During mining, a boundary layer of flow forms in the kerogen, as shown by the textured brown strip. Fluid moves out of the inclusion, indicated by the red arrows. The evolution of the boundary layer, analyzed along the coordinate labeled X, is key to the rate and longevity of the formation’s productivity.
Given that over 20 trillion cubic meters of natural gas, a third of the United States’ total reserves, are thought to be trapped in shale, and given the rush to exploit shale oil and gas resources by Australia, Canada, China, and other countries around the world—even oil-rich Saudi Arabia—it’s a wonder that producers still rely on models of how fluids flow underground that were devised in the heyday of oil and gas development.
Shale is a sedimentary rock thought to be formed from silt deposited in still waters, consisting of layered, fine-grained clay minerals and, often, organic matter such as kerogen, the source of oil and gas. Until now, no mathematical model of gas reservoirs has explicitly incorporated kerogen in calculating how the gas and oil become available and how long a reservoir is liable to keep producing.
The onset of large-scale shale mining calls for a new approach, and the call has been answered by Paulo Monteiro, Chris Rycroft, and Grigory Isaakovich Barenblatt in recent research describing a mathematical model of fluid and gas flow in nanoporous media. Monteiro, Rycroft, and Barenblatt are with the Lab’s Computational Research Division and UC Berkeley’s Department of Civil and Environmental Engineering; Monteiro is also with Berkeley Lab’s Advanced Light Source, and Barenblatt is also with the Russian Academy of Science’s Institute of Oceanology.
The authors studied the physical structure of shales and posited a general structure with two components. One is the fine-clay matrix, ordinary rock with nanoscale pores (pores whose dimensions are measured in billionths of a meter) and fissures. The other is the kerogen inclusions, which contain the majority of the oil and gas. The inclusions may be highly porous, but the oil and gas have a hard time getting out because of the fine pores in the surrounding rock; thus they have very low permeability.
Drilling and mining rapidly reduce pressure on the shale, and even if the pressure difference inside the kerogen inclusion and in the surrounding rock isn’t great, the gradient from inside is steep over a short distance. In this thin boundary layer, things move and break up: pores and tubes open up and grow larger, permeability increases, and fluid begins to flow.
By developing the details of their model, the authors were able to calculate how rapidly a reservoir starting at a certain production level would decline and how long it would remain productive. They then compared their model’s predictions with data from real gas and oil fields, including the Eagle Ford, Austin Chalk, Haynesville, Texas Panhandle, and Barnett fields, and found good agreement.
Since production from shales in this model depends crucially on the increase of permeability at the boundary between matrix and kerogen inclusions, the authors conclude that “Petroleum scientists and engineers should find technological methods to improve the efficiency of the boundary layer further to increase the gas and oil production.
About Computing Sciences at Berkeley Lab
High performance computing plays a critical role in scientific discovery. Researchers increasingly rely on advances in computer science, mathematics, computational science, data science, and large-scale computing and networking to increase our understanding of ourselves, our planet, and our universe. Berkeley Lab’s Computing Sciences Area researches, develops, and deploys new foundations, tools, and technologies to meet these needs and to advance research across a broad range of scientific disciplines.







 Instagram
Instagram YouTube
YouTube