CAMERA Mathematicians Build an Algorithm to ‘Do the Twist’
New Approach Extracts Rotational Diffusion from X-ray Photon Correlation Spectroscopy Experiments
August 18, 2021
Contact: cscomms@lbl.gov
Mathematicians at the Center for Advanced Mathematics for Energy Research Applications (CAMERA) at Lawrence Berkeley National Laboratory (Berkeley Lab) have developed a mathematical algorithm to decipher the rotational dynamics of twisting particles in large complex systems from the X-ray scattering patterns observed in highly sophisticated X-ray photon correlation spectroscopy (XPCS) experiments.
These experiments — designed to study the properties of suspensions and solutions of colloids, macromolecules, and polymers — have been established as key scientific drivers to many of the ongoing coherent light source upgrades occurring within the U.S. Department of Energy (DOE). The new mathematical methods, developed by the CAMERA team of Zixi Hu, Jeffrey Donatelli, and James Sethian, have the potential to reveal far more information about the function and properties of complex materials than was previously possible.
Particles in a suspension undergo Brownian motion, jiggling around as they move (translate) and spin (rotate). The sizes of these random fluctuations depend on the shape and structure of the materials and contain information about dynamics, with applications across molecular biology, drug discovery, and materials science.
XPCS works by focusing a coherent beam of X-rays to capture light scattered off of particles in suspension. A detector picks up the resulting speckle patterns, which contain several tiny fluctuations in the signal that encode detailed information about the dynamics of the observed system. To capitalize on this capability, the upcoming coherent light source upgrades at Berkeley Lab's Advanced Light Source (ALS), Argonne's Advanced Photon Source (APS), and SLAC's Linac Coherent Light Source are all planning some of the world's most advanced XPCS experiments, taking advantage of the unprecedented coherence and brightness.
But once you collect the data from all these images, how do you get any useful information out of them? A workhorse technique to extract dynamical information from XPCS is to compute what’s known as the temporal autocorrelation, which measures how the pixels in the speckle patterns change after a certain passage of time. The autocorrelation function stitches the still images together, just as an old-time movie comes to life as closely related postcard images fly by.
Current algorithms have mainly been limited to extracting translational motions; think of a Pogo stick jumping from spot to spot. However, no previous algorithms were capable of extracting “rotational diffusion" information about how structures spin and rotate — information that is critical to understanding the function and dynamical properties of a physical system. Getting to this hidden information is a major challenge.
Twisting the Light Away
A breakthrough came when experts came together for a CAMERA workshop on XPCS in February 2019 to discuss critical emerging needs in the field. Extracting rotational diffusion was a key goal, and Hu, a UC Berkeley math graduate student; Donatelli, the CAMERA Lead for Mathematics; and Sethian, Professor of Mathematics at UC Berkeley and CAMERA Director, teamed up to tackle the problem head on.
The result of their work is a powerful new mathematical and algorithmic approach to extract rotational information, now working in 2D and easily scalable to 3D. With remarkably few images (less than 4,000), the method can easily predict simulated rotational diffusion coefficients to within a few percent. Details of the algorithm were published August 18 in the Proceedings of the National Academy of Sciences.
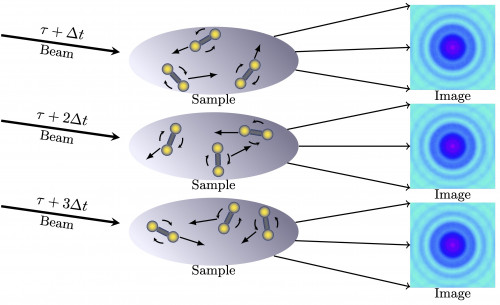
Schematic illustration of the XPCS experiments. The translation and rotation of the particles within the scattering volume leads to variation of the speckle patterns shown on the right. (While the grainy, noise-like texture makes these images appear visually similar, the MTECS algorithm is able to detect and analyze tiny variations between patterns.)
The key idea is to go beyond the standard autocorrelation function, instead seeking the extra information about rotation contained in angular-temporal cross-correlation functions, which compare how pixels change in both time and space. This is a major jump in mathematical complexity: simple data matrices turn into 4-way data tensors, and the theory relating the rotational information to these tensors involves advanced harmonic analysis, linear algebra, and tensor analysis. To relate the desired rotational information to the data, Hu developed a highly sophisticated mathematical model that describes how the angular-temporal correlations behave as a function of the rotational dynamics from this new complex set of equations.
“There were lots of layered mysteries to unravel in order to build a good mathematical and algorithmic framework to solve the problem,” said Hu. “There was information related to both static structures and to dynamic properties, and these properties needed to be systematically exploited to build a consistent framework. Taken together, they present a wonderful opportunity to weave together many mathematical ideas. Getting this approach to pick up useful information out of what seems at first glance to be awfully noisy was great fun.”
However, solving this set of equations to recover the rotational dynamics is challenging, as it consists of several layers of different types of mathematical problems that are difficult to solve all at once. To tackle this challenge, the team built on Donatelli's earlier work on Multi-Tiered Iterative Projections (M-TIP), which is designed to solve complex inverse problems where the goal is to find the input that produces an observed output. The idea of M-TIP is to break a complex problem into subparts, using the best inversion/pseudoinversion you can for each subpart, and iterate through those subsolutions until they converge to a solution that solves all parts of the problem.
Hu and his colleagues took these ideas and built a sister method, “Multi-Tiered Estimation for Correlation Spectroscopy (M-TECS),” solving the complex layered set of equations through systematic substeps.
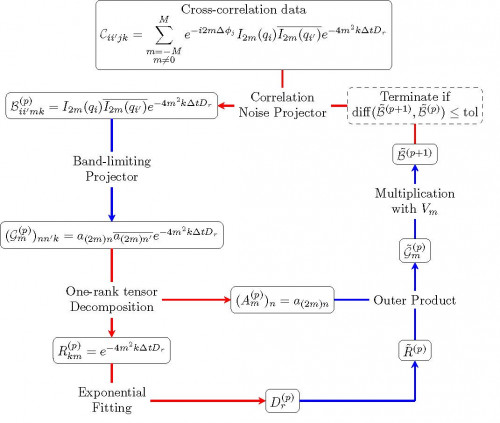
Schematic illustration of the M-TECS algorithm for determining the rotational diffusion coefficient of a dynamical system from its XPCS cross-correlation data. M-TECS works by splitting up the inversion into subparts, each of which of efficient mathematical tricks for inverting/pseudoinverting, and then iterating over those subparts until convergence to the correct solution.
“The powerful thing about the M-TECS approach is that it exploits the fact that the problem can be separated into high-dimensional linear parts and low-dimensional nonlinear and nonconvex parts, each of which have efficient solutions on their own, but they would turn into an exceedingly difficult optimization problem if they were instead to be solved for all at once,” said Donatelli.
“This is what enables M-TECS to efficiently determine rotational dynamics from such a complex system of equations, whereas standard optimization approaches would run into trouble both in terms of convergence and computational cost.”
Opening the Door to New Experiments
"XPCS is a powerful technique that will feature prominently in the ALS upgrade. This work opens up a new dimension to XPCS, and will allow us to explore the dynamics of complex materials such as rotating molecules inside water channels," said Alexander Hexemer, Program Lead for Computing at the ALS.
Hu, who won UC Berkeley's Bernard Friedman Prize for this work, has joined CAMERA — part of Berkeley Lab’s Computational Research Division — as its newest member. “This sort of mathematical and algorithmic co-design is the hallmark of good applied mathematics, in which new mathematics plays a pivotal role in solving practical problems at the forefront of scientific inquiry," said Sethian.
The CAMERA team is currently working with beamline scientists at the ALS and APS to design new XPCS experiments that can fully leverage the team’s mathematical and algorithmic approach to study new rotational dynamics properties from important materials. The team is also working on extending their mathematical and algorithmic framework work to recover more general types of dynamical properties from XPCS, as well as apply these methods to other correlation imaging technologies.
This work is supported by CAMERA, which is jointly funded by the Office of Advanced Scientific Computing Research and the Office of Basic Energy Sciences, both within the U.S. Department of Energy’s Office of Science.
About Computing Sciences at Berkeley Lab
High performance computing plays a critical role in scientific discovery. Researchers increasingly rely on advances in computer science, mathematics, computational science, data science, and large-scale computing and networking to increase our understanding of ourselves, our planet, and our universe. Berkeley Lab’s Computing Sciences Area researches, develops, and deploys new foundations, tools, and technologies to meet these needs and to advance research across a broad range of scientific disciplines.







 Instagram
Instagram YouTube
YouTube