Deep Learning Tactics Speed Quantum Simulations
Researchers put spin on tried and true methods to enhance many-body control
October 4, 2021
Contact: cscomms@lbl.gov
Machine learning is emerging as a useful tool in the development of quantum computing platforms, particularly in optimizing the methodologies used to simulate quantum systems and speed the time it takes to create and test different approaches and designs.
A key challenge, however, is being able to prepare a quantum-mechanical system in its ground state – that is, its lowest-energy state. Solving the ground state preparation problem would enable researchers to investigate the existence of novel quantum phases of matter and open the door to innovative applications – including high-temperature superconductors, magnetic field sensors, and synthetic molecules – based on quantum phenomena.
To make this happen, researchers are looking at combinations of old and new mathematical and physical techniques to solve fundamental issues such as many-body control. A new paper published September 30 in Physical Review X outlines an algorithm that blends variational quantum algorithms with reinforcement learning, a powerful technique for training machine learning models to make a sequence of decisions.
“We believe this work is very timely in the context of quantum computing and presents a potential paradigm shift in developing and understanding the performance of certain quantum algorithms for many-body quantum physics,” said co-author Lin Lin, a faculty scientist in the Applied Math and Computational Research Division at Lawrence Berkeley National Laboratory and an associate professor in the Department of Mathematics at the University of California, Berkeley (UC Berkeley).
Variational quantum algorithms have gained favor in recent years because of their ability to use near-term quantum computers to solve certain optimization problems. Since first being introduced in 2014, the Quantum Approximate Optimization Algorithm (QAOA) – which uses both classical and quantum resources to find the approximate solution to combinatorial optimization problems – have attracted attention because they offer a simple model that can be implemented even on noisy intermediate-scale quantum devices (NISQs), Lin noted.
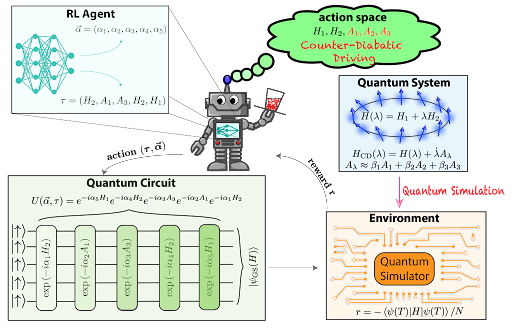
An illustration of a CD-QAOA reinforcement learning agent serving the “water.″ The goal for the agent is to prepare the ground state with high fidelity using counterdiabatic theory. The autoregressive neural network policy is improved via a policy gradient algorithm in the feedback loop between the classical computer and the quantum simulator.
“The idea is to use quantum systems to simulate the behavior of other quantum systems,” said co-author Marin Bukov of the Department of Physics at UC Berkeley and the University of Sofia in Bulgaria. “Basically, if you have a quantum simulator and you can program it in such a way as to get access to the state of a quantum material, you are typically interested in the properties of a specific state of that quantum system. So the bigger question we are addressing in our work is: how do you prepare such a particular state on one of these potential devices?”
Counter-Diabatic Drivers Speed the Process
Toward this end, Bukov, Lin, and lead author Jiahao Yao of the Department of Mathematics at UC Berkeley developed their own hybrid control algorithm, CD-QAOA, which is inspired by the counter-diabatic (CD) driving procedure designed for quantum many-body systems. Adiabaticity is a concept first developed in thermodynamics to describe the state of a system that changes so slowly there are no excitations. Adiabatic evolution, therefore, takes a considerable amount of time. Counterdiabatic drives achieve the same change in the state, just much faster.
Following an analogy in a recent article in the Proceedings of National Academy of Sciences, the authors liken CD driving to a waiter moving a cup of water from one table to another without spilling it. “If you know there is a lot of water in the glass and it is likely to spill, you move very, very carefully so that at each step the water pretty much remains static,” Lin explained. “But if you rush, you will spill the water. So this is what waiters do in the real world: they tilt the tray slightly, which allows them to move fast without spilling the water.”
In the context of quantum mechanics, “the counterdiabatic approach enables us to efficiently prepare a quantum state without ending in a state we don’t want the system to be in,” he added. “This is the basic idea behind the concept of CD driving.”
The CD driving component of the CD-QAOA algorithm is also critical because it generalizes the QAOA algorithm with a larger action space based on variational counter-diabatic theory. This provides users an extra degree of freedom/flexibility – which decreases the quantum simulation time, noted Yao. “This is very desirable because the longer the circuit running time, the larger the error that will accumulate,” he said.
The Reinforcement Learning Twist
Applying reinforcement learning enables optimization of additional parameters and opens new opportunities for exploring large spaces with control protocols. In reinforcement learning, an agent is trying to order the sequence of the different CD actions, Bukov explained. “It is a complex and high-dimensional combinatorial task that is not just doing the intrinsic QAOA optimization but also figuring out the right order in which to construct the control protocol.”
“The combination of reinforcement learning with quantum materials and quantum state control is a connection that has never been very intimate,” Lin added. “One significant progress we made in this paper was to combine them and demonstrate that reinforcement learning can be a very useful tool for exploring a large control space so that you can control these quantum states much more efficiently.”
Other research groups are pursuing similar tactics to address the challenges of many-body control in quantum systems research. A recent study published in Nature Quantum Information used a neural network and QAOA to parameterize the quantum wave functions and further simulate the quantum dynamics on a classical computer. Similarly, a paper published in April in Physical Review A introduces an algorithmic framework for digital quantum control designed to enhance quantum information processing. While the end goals are similar, these approaches differ from the model that Yao, Lin, and Bukov have developed.
“Our algorithm is a quantum-classical hybrid method that uses a quantum simulator/computer to run the quantum dynamics and classical computers to run the machine learning algorithms and variationally tune the parameters for the quantum circuits,” Yao explained.
At its core, Bukov added, this research is about understanding many-body physics – i.e., how many quantum degrees of freedom interact, which is a current bottleneck in designing scalable quantum simulators. “You can only have interactions if you have more than one particle or qubit. For a realistic quantum simulation, you need a regime where you can control a large number of interacting degrees of freedom,” he said.
“We see this as a new beginning” in this area of research, Lin said. “There is a very generic way to think about these control problems, but wherever the QAOA type of thing has been considered by previous researchers, we invite them to think about whether there is a way to employ CD principles to dramatically speed up the process and/or improve the accuracy.”
This work is partly supported by the Quantum Algorithms Team, the DOE Early Career award, the Accelerated Research in Quantum Computing (ARQC) program funded by the Office of Advanced Scientific Computing Research within the U.S. Department of Energy’s Office of Science, the Quantum Leap Challenge Institute (QLCI) program funded by the National Science Foundation, the Gordon and Betty Moore Foundation, and the Bulgarian National Science Fund.
About Computing Sciences at Berkeley Lab
High performance computing plays a critical role in scientific discovery. Researchers increasingly rely on advances in computer science, mathematics, computational science, data science, and large-scale computing and networking to increase our understanding of ourselves, our planet, and our universe. Berkeley Lab’s Computing Sciences Area researches, develops, and deploys new foundations, tools, and technologies to meet these needs and to advance research across a broad range of scientific disciplines.







 Instagram
Instagram YouTube
YouTube