Berkeley Lab AI Autonomously Steers Data Acquisition at Neutron Scattering Facility in France
Self-learning algorithm developed by CAMERA researchers breaks new ground in data collection and analysis
October 6, 2020
Contact: cscomms@lbl.gov
A self-learning algorithm developed at Lawrence Berkeley National Laboratory (Berkeley Lab) has enabled researchers at the Institut Laue-Langevin (ILL) in Grenoble, France to run an autonomous data analysis during a neutron scattering experiment at ThALES, the three-axis low energy spectrometer project that is a collaboration between ILL and Charles University in Prague, Czech Republic.
During the second reactor cycle in 2020, the ThALES team and SCI/CS at ILL commissioned and tested the gpCAM algorithm, created by researchers at Berkeley Lab’s Center for Advanced Mathematics for Energy Research Applications (CAMERA). For the first time at ILL, the algorithm took control over the measurement process without human intervention. Completely agnostic – without any prior information on the physical model or expected signal of the measured sample – the algorithm explored various accessible instrument regions and reconstructed the signal with a strongly reduced number of total measuring points compared to the conventional grid scanning technique.
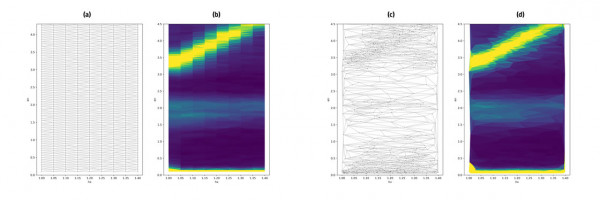
Comparison of a classical grid scan measurement (a, b) with a data collection, controlled by the autonomous algorithm gpCAM (c, d) on ThALES. Dots in figures a and b show the selected points, figures b and d show the intensity distribution with Delaunay triangular interpolation between measured points.
Today’s news is filled with stories about progress on machine learning or artificial intelligence in all aspects of life, be it self-driving cars, mobile applications, or face or speech recognition systems such as Siri, Alexa, or Google home. Most of the algorithms behind these applications fall into the category of so-called supervised learning, where the algorithms are trained on a huge amount of data (big data) to classify images or sound patterns. Similar techniques could also accelerate the data analysis for instruments with large data acquisition rates, as recently discussed in a joint ILL/ESRF workshop on Artificial Intelligence.
Compared to the previously mentioned applications of big data, the data sets from synchrotron or neutron experiments are orders of magnitude smaller (typically in the mega or gigabyte range). Nevertheless, some of the big-data learning algorithms have already successfully been applied to data sets taken from neutron spectrometers.
While the technical improvements have led to the ability to collect ever-larger data sets on most modern scientific instruments, the power of a triple-axis spectrometer (TAS) lies not in the amount of data that it collects, but in the strength and efficiency with which it measures very specific data (for example, for specific transfers of momentum and energy for parameters such as pressure or magnetic field). In this respect, contrary to big data applications, TAS data sets are smaller and the information density is higher. Therefore, for an efficient experiment, it is particularly important that measurements are well-targeted – that is, data is taken at meaningful points – and that no time is wasted to obtain information that later turns out to be irrelevant.
A promising route lies in autonomous learning, where algorithms such as gpCAM – developed by Marcus Noack of the CAMERA team – learn from a comparatively little amount of input data and decide themselves on the next steps to take. The main ingredients in gpCAM are a flexible Gaussian process engine and a powerful mathematical optimization, which is used to train the process but also to find the next optimal measurement points.
Use the slider to compare the classical grid scan measurement with a data collection controlled by the autonomous algorithm gpCAM on ThALES. (Interactive illustration created with Flourish.)
“A Gaussian process takes advantage of a Gaussian probability density over functions, one of the most fundamental ideas in mathematics, combined with a powerful optimization technique,” Noack explained. “The key to a successful Gaussian process is to learn an optimal prior probability density over functions and condition it on the collected data.”
In the Bayesian language, gpCAM estimates the posterior mean and covariance and uses them in a function optimization to calculate the optimal next measurement point. The posterior is based on a prior Gaussian probability density function, which is repeatedly retrained on previously measured points.
The Kriging Model
The algorithm is known as the Kriging model in the geosciences, named after Danie G. Krige, a South African geologist who sought to estimate the most likely distribution of gold from a few boreholes in the Witwatersrand reef complex in South Africa.
Sometimes, this task resembles the situation in an experiment; the meaningful inelastic neutron scattering intensity S(Q,ω) might be distributed like gold veins defined by the momentum Q and energy hω transfer, and the experimenter does not know where to look next. Moreover, while the gold seeker moves across a two-dimensional space (the land) when choosing a place to drill, the space defined by momentum and energy transfer is four-dimensional.
It is a surprisingly neglected practice to quantify measuring probabilities based on statistical or Bayesian methods or, simply speaking, a surprisingly neglected question, how many individual measuring points S(Qi,ωi) are needed to either acquire sufficient information – whether it be in the agnostic case, or to confirm pre-established theoretical models.
A glance at published work suggests that the amount of meaningful data is of the order of kbytes or less, rather than Gbytes or more. The measurement time for hundreds of (meaningful) points on a TAS is of the order of hours, compared to several days in the traditional setting, which shows the optimization potential of an assisting autonomous algorithm. Already in the very first test runs, without any specific tuning of kernel definitions and acquisition functions, the algorithm demonstrated its efficiency as shown in the example below, where a conventional grid-scan on a magnetic excitation is compared to various intermediate states of the gpCAM acquisition. In addition, the results were achieved without human supervision or interaction.
ILL's next goal is to assist gpCAM with the implementation of previously known information like crystal symmetry or even theoretical models, in order to reduce the number of points and to increase the efficiency of the measurement even further.
“These sorts of co-design teams between applied mathematicians and experimentalists greatly accelerate the development of practical tools that merge new mathematics with rapidly evolving, complex experiments,” said James Sethian, director of CAMERA.
In addition to Noack and Sethian, members of this collaborative effort include Martin Boehm, Paul Steffens, and Emmanuel Villard at ThALES and Tobias Weber, Y. LeGoc, and Paolo Mutti at ILL-CS/SCI.
This article is adapted from an ILL news release.
About Computing Sciences at Berkeley Lab
High performance computing plays a critical role in scientific discovery. Researchers increasingly rely on advances in computer science, mathematics, computational science, data science, and large-scale computing and networking to increase our understanding of ourselves, our planet, and our universe. Berkeley Lab’s Computing Sciences Area researches, develops, and deploys new foundations, tools, and technologies to meet these needs and to advance research across a broad range of scientific disciplines.







 Instagram
Instagram YouTube
YouTube