Math for Data
Berkeley Lab designs, builds, and applies the core mathematical tools needed to understand scientific data. This includes new techniques for such varied tasks as solving complex inverse problems to reconstruct models from measured experimental or simulation data; developing surrogate models and reduced order approximations to encapsulate key structures and characteristics; compressing data in compact forms with minimal loss of information; image and signal analysis, exploiting new methods in computer vision and machine learning/artificial intelligence; and applying on-the-fly measured or computed data in designing autonomous, self-driving experiments.
Our teams work directly with experimentalists throughout DOE, academia, and national and international labs to identify and address key mathematical challenges in the experimental sciences. We develop new mathematical frameworks encompassing computational harmonic analysis, numerical linear algebra, computational topology, optimization, stochastic function approximation theory, Gaussian processes, statistics, signal and image processing, computer vision, artificial intelligence, and machine learning. These solutions are coupled with high-performance computing and user-friendly software to meet the needs of scientific users.
Our revolutionary new mathematics have solved several long-standing, open problems in reconstructing structure and dynamics of biological objects and materials from microscopy and scattering data; enabled human-free autonomous steering of experiments, accelerated analysis and increased scientific output of experiments by several orders of magnitude; and allowed machine-learning-based image recognition and classification to be performed with extremely limited training data. These mathematical solutions are being used to enable new scientific breakthroughs in biology, materials science, and physics.
Projects
Fluctuation Scattering and Single-Particle Diffraction from X-ray Free-Electron Lasers
Fluctuation X-ray scattering (FXS) and single-particle diffraction (SPD) are emerging experimental techniques that leverage the capabilities of X-ray free-electron lasers to capture new information about the 3D structure and dynamics of uncrystallized biological samples that cannot be probed using previous techniques. However, in these experiments the particle samples are imaged at random and unknown orientations and the data is heavily corrupted by noise and background, which have served as a major barrier in analyzing the data. We have developed a new mathematical framework called Multi-Tiered Iterative Projections (M-TIP) that can fully exploit the mathematical substructures of these subproblems and has provided the first solution to the open problem of FXS reconstruction and greatly reduced the amount of SPD data required for an accurate reconstruction. We are currently working with teams from the SLAC National Accelerator Laboratory and Los Alamos National Lab, as part of the ExaFEL exascale computing project, to scale these M-TIP algorithms on DOE’s next generation of supercomputers to enable real-time analysis of FXS and SPD experiments at the Linac Coherent Light Source. Contacts: Jeffrey Donatelli, Kanupriya Pande, Peter Zwart
3D Reconstruction from Coherent Surface Scattering Imaging
Coherent surface scattering imaging (CSSI) is an emerging experimental technique for imaging thin samples placed on a substrate by collecting a series of X-ray diffraction patterns collected at grazing-incident angles using a coherent X-ray beam. However, determining 3D structure from CSSI data has been an open problem due to the presence of multiple-scattering events, involving both the sample and substrate, which greatly complicates the analysis. We have developed a new mathematical framework that couples new work in Multi-Tiered Iterative Projections (M-TIP) and nonuniform fast Fourier transform inversion and provides the first solution to the CSSI reconstruction problem. We are collaborating with scientists at Argonne National Lab to extend and apply this framework to determine material structure from new CSSI experiments at the Advanced Photon Source. Contact: Jeffrey Donatelli
Structure Determination from Multiple-Scattering Electron Crystallography
Transmission electron diffraction of crystals is a powerful tool for imaging the atomic structure of crystals that cannot be made large enough to scatter sufficient signal using other diffraction-based techniques. However, standard analysis techniques start to break down for crystals larger than about 10 nm in size, due to the presence of multiple-scattering events, where the electrons in the beam interact with several different atoms in the sample before being measured. In collaboration with Arizona State University, we have developed a new approach, called N-Phaser, based on the Multi-Tiered Iterative Projection (M-TIP) framework, that enables one to reconstruct crystal structure from multiple-scattering electron crystallography data from arbitrarily large crystals. We are currently working on extending the N-phaser framework to capture more complex physics in the experiment and extend it to treat multiple-scattering artifacts in other experimental techniques. Contact: Jeffrey Donatelli
gpCAM for Domain-Aware Autonomous Experimentation
gpCAM is an API and software designed to make autonomous data acquisition and analysis for experiments and simulations faster, simpler, and more widely available. The tool is based on a flexible and powerful Gaussian process regression at the core. The flexibility stems from the modular design of gpCAM, which allows the user to implement and import their own Python functions to customize and control almost every aspect of the software. That makes it possible to easily tune the algorithm to account for various kinds of physics and other domain knowledge, and to identify and find interesting features and function characteristics. A specialized function optimizer in gpCAM can take advantage of HPC architectures for fast analysis time and reactive autonomous data acquisition. Contact: Marcus Noack
HGDL for Hybrid Global Deflated Local Optimization
HGDL is an optimization algorithm specialized in finding not just one but a diverse set of optima, alleviating challenges of non-uniqueness that are common in modern applications such as inversion problems and training of machine learning models. HGDL is customized for distributed high-performance computing; all workers can be distributed across as many nodes or cores. All local optimizations will then be executed in parallel. As solutions are found they are deflated, which effectively removes those optima from the function so that they cannot be reidentified by subsequent local searches. Contact: Marcus Noack
Joint Iterative Reconstruction and 3D Rigid Alignment for X-ray Tomography
The technique of tomography consists of reconstructing the three-dimensional (3D) map (tomogram) of an object from its two-dimensional (2D) projections collected when the object is rotated about one or more axes. A fundamental underlying assumption in the reconstruction procedure is that the relative orientation of the beam, sample and detector is known exactly. In practice however, misalignments in data are induced due to mechanical instability of the sample stage, drifts in the illuminating radiation and sample deformation as a result of inherent dynamics. We have recently developed a new algorithm for joint iterative reconstruction and 3D alignment of X-ray tomography data that recovers accurate rigid body motions by minimizing inconsistencies between measured projection data and model data obtained by applying the forward projection operator to the reconstructed object. Contact: Kanupriya Pande
TomoCAM: GPU-accelerated Model-Based Iterative Tomographic Reconstruction
We have developed a new mathematical framework and the software package, TomoCAM, which leverages non-uniform fast Fourier transforms (NUFFT) and graphics processing unit (GPU) architecture to implement model-based iterative reconstruction (MBIR) that allows high quality tomographic reconstructions on a desktop hardware, eliminating the need for a large cluster. The subroutines are optimized to maximize throughput to GPU devices. A python interface is provided to drive computations via a Jupyter notebook framework, which is popular within the material science community. Contact: Dinesh Kumar
Protein Conformation Reconstruction from Diffuse X-ray Scattering
In X-ray crystallography, the Bragg peaks encode information on the average electron density of all molecules in a crystal, while the smoothly varying diffuse signal contains information about the spatial correlations of the electron density variations. Analysis of diffuse signal is challenging since the signal itself is weak and appears as small fluctuations on top of the background. As such, conventional structure solution techniques discard the diffuse signal and treat only Bragg peaks, thereby yielding an ensemble averaged structure. We have developed mathematical theory to describe a diffraction model for diffuse X-ray scattering that accounts for the presence of multiple protein conformations and developed an algorithmic framework based on iterative projection algorithms and constrained optimization to reconstruct different conformations that give rise to diffuse scattering. Contact: Kanupriya Pande
Extraction of Rotational Dynamics from X-ray Photon Correlation Spectroscopy
X-ray photon correlation spectroscopy (XPCS) is a powerful technique for probing dynamics in a wide range of space and time scale. Though the required raw data is accessible from XPCS experiments, there was no good algorithm before for extracting the rotational dynamics, whose analysis is a classic problem in many research fields. To handle this task, we have developed “Multi-Tiered Estimation for Correlation Spectroscopy” algorithm, which is the first algorithm to estimate the two-dimensional rotational diffusion coefficients of non-spherical particles with arbitrary shape based on XPCS. To build such algorithm, we introduced a new analysis tool, the angular-temporal cross-correlation, that can provide high dimensional data tensor containing much more than the conventional correlation analysis. By including additional data filtering techniques, the MTECS algorithm is robust against noisy data. Currently, we are working on adapting the MTECS algorithm to estimate the three-dimensional fully-anisotropic rotational diffusion tensors. Contact: Zixi Hu
Hybrid-Global-Deflated-Local Optimization for Finding Diverse Sets of Optima
HGDL is an optimization algorithm specialized in finding not just one but a diverse set of optima, alleviating challenges of non-uniqueness that are common in modern applications such as inversion problems and training of machine learning models. HGDL is customized for distributed high-performance computing; all workers can be distributed across as many nodes or cores. All local optimizations will then be executed in parallel. As solutions are found they are deflated, which effectively removes those optima from the function so that they cannot be reidentified by subsequent local searches. Contact: Marcus Noack
Mixed-Scale Neural Networks for Image Analysis from Limited Training Data
Mathematicians at Berkeley Lab’s Center for Advanced Mathematics for Energy Research Applications (CAMERA) are turning the usual machine learning perspective on its head using a mixed-scale convolution neural networks that requires far fewer parameters than traditional methods, converges quickly, and has the ability to learn from a remarkably small training set. Combing new approaches building on our earlier work, such as randomized architectures and uncertainty quantification, these methods allow for rapid extraction of scientific data from a wide variety of imaging data. Contacts: James Sethian, Dinesh Kumar, Peter Zwart
Dionysus
Dionysus is a library for computing persistent homology. It implements an extensive collection of algorithms used in topological data analysis. Contact: Dimitriy Morozov
Machine Learning with Persistent Homology of Guest Adsorption in Nanoporous Materials
We use persistent homology to describe the geometry of nanoporous materials at various scales. We combine our topological descriptor with traditional structural features and investigate the relative importance of each to the prediction tasks. Our results not only show a considerable improvement compared to the baseline, but they also highlight that topological features capture information complementary to the structural features. Furthermore, by investigation of the importance of individual topological features in the model, we are able to pinpoint the location of the relevant pores, contributing to our atom-level understanding of structure-property relationships. Contact: Dimitriy Morozov
Topological Optimization with Big Steps
Using persistent homology to guide optimization has emerged as a novel application of topological data analysis. Existing methods treat persistence calculation as a black box and backpropagate gradients only to critical points. We show how to extract more information from the persistence calculation and prescribe gradients to larger subsets of the domain. We present empirical experiments that show the practical benefits of our algorithm: the number of steps required for the optimization is reduced by an order of magnitude. Contact: Dimitriy Morozov
News
CAMERA Mathematicians Build an Algorithm to ‘Do the Twist’
CAMERA mathematicians have developed an algorithm to decipher the rotational dynamics of twisting particles in large complex systems from the X-ray scattering patterns observed in X-ray photon correlation spectroscopy experiments. Read More »

Machine Learning Algorithms Help Predict Traffic Headaches
A team of Berkeley Lab computer scientists is working with the California Department of Transportation and UC Berkeley to use high performance computing and machine learning to help improve Caltrans’ real-time decision making when traffic incidents occur. Read More »

Berkeley Lab’s CAMERA Leads International Effort on Autonomous Scientific Discoveries
To make full use of modern instruments and facilities, researchers need new ways to decrease the amount of data required for scientific discovery and address data acquisition rates humans can no longer keep pace with. Read More »

New Algorithm Enhances Ptychographic Image Reconstruction
Researchers from CAMERA, the University of Texas and Tianjin Normal University have developed an algorithmic model that enhances the image reconstruction capabilities of Berkeley Lab's SHARP algorithmic framework and computer software that is used to reconstruct millions of phases of ptychographic image data per second. Read More »

Math of Popping Bubbles in a Foam
Researchers from the Department of Energy’s (DOE’s) Lawrence Berkeley National Laboratory (Berkeley Lab) and the University of California, Berkeley have described mathematically the successive stages in the complex evolution and disappearance of foamy bubbles, a feat that could help in modeling industrial processes in which liquids mix or in the formation of solid foams such as those used to cushion bicycle helmets. Read More »
Advancing New Battery Design with Deep Learning
A team of researchers from Berkeley Lab and UC Irvine has developed deep-learning algorithms designed to automate the quality control and assessment of new battery designs for electric cars. Read More »
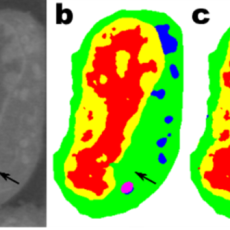
Berkeley Lab “Minimalist Machine Learning” Algorithms Analyze Images from Very Little Data
Berkeley Lab mathematicians have developed a new approach to machine learning aimed at experimental imaging data. Rather than relying on the tens or hundreds of thousands of images used by typical machine learning methods, this new approach “learns” much more quickly and requires far fewer images. Read More »

International Team Reconstructs Nanoscale Virus Features from Correlations of Scattered X-rays
Berkeley Lab researchers contributed key algorithms which helped scientists achieve a goal first proposed more than 40 years ago – using angular correlations of X-ray snapshots from non-crystalline molecules to determine the 3D structure of important biological objects. Read More »

New Berkeley Lab Algorithms Extract Biological Structure from Limited Data
A new Berkeley Lab algorithmic framework called multi-tiered iterative phasing (M-TIP) utilizes advanced mathematical techniques to determine 3D molecular structure of important nanoobjects like proteins and viruses from very sparse sets of noisy, single-particle data. Read More »

New Mathematics Advances the Frontier of Macromolecular Imaging
Berkeley Lab researchers have introduced new mathematical theory and an algorithm, which they call "Multi-tiered iterative phasing (M-TIP)," to solve the reconstruction problem from fluctuation X-ray scattering data. This approach is an important step in unlocking the door to new advances in biophysics and has the promise of ushering in new tools to help solve some of the most challenging problems in the life sciences. Read More »







 Instagram
Instagram YouTube
YouTube